Aufgaben zum Einfluss der Parameter a, b und c auf die Parabel

Hier lernst du, wie die Parameter $a$ , $b$ und $c$ aus dem quadratischen Funktionsterm $f (x) = a x^{2} + b x + c$ den Verlauf der Parabel beeinflussen.

1
Betrachte das Applet und verändere den Öffnungsfaktor $a$ des Funktionsgraphen von $y = a \cdot x^{2}$ . Beobachte, wie sich der Funktionsgraph verändert und beantworte dann die folgenden Fragen. In grau siehst du den Funktionsgraph der Normalparabel.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
Bei $0 < a < 1$ ist der Funktionsgraph der Parabel $y = a \cdot x^{2}$
breiter als die Normalparabel, die Parabel ist also gestaucht.
enger als die Normalparabel, die Parabel ist also gestreckt.
genau der Funktionsgraph der Normalparabel.

Bei $a = 1$ ist der Funktionsgraph der Parabel $y = a \cdot x^{2}$
genau der Funktionsgraph der Normalparabel.
enger als die Normalparabel, die Parabel ist also gestreckt.
breiter als die Normalparabel, die Parabel ist also gestaucht.

Bei $a > 1$ ist der Funktionsgraph der Parabel $y = a \cdot x^{2}$
enger als die Normalparabel, die Parabel ist also gestreckt.
breiter als die Normalparabel, die Parabel ist also gestaucht.
genau der Funktionsgraph der Normalparabel.
2
Verändere den Öffnungsfaktor $a$ ins Negative und beobachte, wie sich der Funktionsgraph ändert! Beantworte anschließend die Fragen. In grau siehst du den Funktionsgraphen der Normalparabel.
Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unsererDatenschutzerklärung.
Wähle alle richtigen Aussagen aus:
Der Funktionsgraph von $y = - a \cdot x^{2}$ ist der an der $x$ -Achse gespiegelte Funktionsgraph von $y = a \cdot x^{2}$ .
Wenn der Öffnungsfaktor $a$ negativ ist, dann ist die Parabel nach unten geöffnet.
Der Funktionsgraph von $y = - a \cdot x^{2}$ ist der an der $y$ -Achse gespiegelte Funktionsgraph von $y = a \cdot x^{2}$ .
Wenn der Öffnungsfaktor $a$ negativ ist, ist die Parabel nach oben geöffnet.

Bei $- 1 < a < 0$ ist der Funktionsgraph der Parabel $y = a \cdot x^{2}$
nach unten geöffnet und breiter als die Normalparabel, also gestaucht.
nach unten geöffnet und enger als die Normalparabel, also gestreckt.
der Funktionsgraph der Normalparabel an der $x$ -Achse gespiegelt.

Bei $a = - 1$ ist der Funktionsgraph der Parabel $y = a \cdot x^{2}$
der Funktionsgraph der Normalparabel an der $x$ -Achse gespiegelt.
nach unten geöffnet und breiter als die Normalparabel, also gestaucht.
nach unten geöffnet und enger als die Normalparabel, also gestreckt.

Bei $a < - 1$ ist der Funktionsgraph der Parabel $y = a \cdot x^{2}$
nach unten geöffnet und enger als die Normalparabel, also gestreckt.
nach unten geöffnet und breiter als die Normalparabel, also gestaucht.
der Funktionsgraph der Normalparabel an der $x$ -Achse gespiegelt.

Betrachtet werden quadratische Funktionen, bei denen die Funktionsgleichung in der allgemeinen Form $f (x) = a \cdot x^{2} + b \cdot x + c$ gegeben ist.

Wie verschiebt sich der Funktionsgraph $G_{f}$ der Funktion $f (x) = 2 \cdot x^{2} + 8 \cdot x + 4$ , wenn der Parameter $b$ um 1 erhöht bzw. um 1 reduziert wird?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Parabel

Die Ausgangsfunktion lautet: $f (x) = 2 \cdot x^{2} + 8 \cdot x + 4$ .

Der Graph $G_{f}$ ist eine Parabel und in der Abbildung $grün$ gezeichnet.

Bei dieser Funktion hat der Parameter $b$ den Wert $8$ .

Erhöhst du den Parameter $b$ um 1, so lautet nun die Funktionsgleichung $g (x) = 2 \cdot x^{2} + 9 \cdot x + 4$ .

Der Graph $G_{g}$ ist in der Abbildung $rot$ gezeichnet.

Reduzierst du den Parameter $b$ um 1, so lautet nun die Funktionsgleichung $h (x) = 2 \cdot x^{2} + 7 \cdot x + 4$ .

Der Graph $G_{h}$ ist in der Abbildung $violett$ gezeichnet.

Lageuntersuchung der 3 Parabeln

Maßgeblich für die Lage im Koordinatensystem ist der Scheitelpunkt der Parabel. Um die Auswirkungen der Veränderung des Parameters $b$ feststellen zu können, musst du die Scheitelpunkte der $3$ Parabeln berechnen.

Scheitelpunktsberechnung für $f (x)$ :

Wandle die gegebene allgemeine Form $f (x) = 2 \cdot x^{2} + 8 \cdot x + 4$ in die Scheitelform um und lies den Scheitelpunkt ab.

$f (x)$	$=$	$2 \cdot x^{2} + 8 \cdot x + 4$
	↓	2 ausklammern
	$=$	$2 \cdot (x^{2} + 4 x + 2)$
	↓	quadratische Ergänzung
	$=$	$2 \cdot (x^{2} + 4 x + 4 - 4 + 2)$
	↓	die ersten 3 Terme in der Klammer mit binomischer Formel zusammenfassen
	$=$	$2 \cdot ((x + 2)^{2} - 4 + 2)$
	↓	die letzten beiden Terme in der Klammer zusammenfassen
	$=$	$2 \cdot ((x + 2)^{2} - 2)$
	↓	Klammer ausmultiplizieren
	$=$	$2 \cdot (x + 2)^{2} - 4$

Der Scheitelpunkt des Funktionsgraphen $G_{f}$ $(grüne Parabel)$ lautet: $S_{f} (- 2 | - 4)$

Scheitelpunktsberechnung für $g (x)$ :

Die allgemeine Form $g (x) = 2 \cdot x^{2} + 9 \cdot x + 4$ wird in die Scheitelform umgewandelt und der Scheitelpunkt wird abgelesen.

$g (x)$	$=$	$2 \cdot x^{2} + 9 \cdot x + 4$
	↓	2 ausklammern
	$=$	$2 \cdot (x^{2} + 4,5 x + 2)$
	↓	quadratische Ergänzung
	$=$	$2 \cdot (x^{2} + 4,5 x + {2,25}^{2} - {2,25}^{2} + 2)$
	↓	die ersten 3 Terme in der Klammer mit binomischer Formel zusammenfassen
	$=$	$2 \cdot ((x + 2,25)^{2} - 5,0625 + 2)$
	↓	die letzten beiden Terme in der Klammer zusammenfassen
	$=$	$2 \cdot ((x + 2,25)^{2} - 3,0625)$
	↓	Klammer ausmultiplizieren
	$=$	$2 \cdot (x + 2,25)^{2} - 6,125$

Der Scheitelpunkt des Funktionsgraphen $G_{g}$ $(rote Parabel)$ lautet: $S_{g} (- 2,25 | - 6,125)$

Ergebnis: Wird $b$ um $1$ erhöht, so verschiebt sich der Scheitelpunkt der $roten Parabel$ $S_{g} (- 2,25 | - 6,125)$ im Vergleich zum Scheitelpunkt der $grünen Parabel$ $S_{f} (- 2 | - 4)$ .

In x-Richtung ist die $rote Parabel$ ist im Vergleich zur $grünen Parabel$ um $- 0,25$ (d.h. nach links) verschoben.

In y-Richtung ist die $roten Parabel$ im Vergleich zur $grünen Parabel$ um $- 2,125$ (d.h. nach unten) verschoben.

Scheitelpunktsberechnung für $h (x)$ :

Die allgemeine Form $h (x) = 2 \cdot x^{2} + 7 \cdot x + 4$ wird in die Scheitelform umgewandelt und der Scheitelpunkt wird abgelesen.

$h (x)$	$=$	$2 \cdot x^{2} + 7 \cdot x + 4$
	↓	2 ausklammern
	$=$	$2 \cdot (x^{2} + 3,5 x + 2)$
	↓	quadratische Ergänzung
	$=$	$2 \cdot (x^{2} + 3,5 x + {1,75}^{2} - {1,75}^{2} + 2)$
	↓	die ersten 3 Terme in der Klammer mit binomischer Formel zusammenfassen
	$=$	$2 \cdot ((x + 1,75)^{2} - 3,0625 + 2)$
	↓	die letzten beiden Terme in der Klammer zusammenfassen
	$=$	$2 \cdot ((x + 1,75)^{2} - 1,0625)$
	↓	Klammer ausmultiplizieren
	$=$	$2 \cdot (x + 1,75)^{2} - 2,125$

Der Scheitelpunkt des Funktionsgraphen $G_{h}$ $(violette Parabel)$ lautet: $S_{h} (- 1,75 | - 2,125)$

Ergebnis: Wird $b$ um $1$ reduziert, so verschiebt sich der Scheitelpunkt der $violetten Parabel$ $S_{h} (- 1,75 | - 2,125)$ im Vergleich zum Scheitelpunkt der $grünen Parabel$ $S_{f} (- 2 | - 4)$ .

In x-Richtung ist die $violette Parabel$ ist im Vergleich zur $grünen Parabel$ um $0,25$ (d.h. nach rechts) verschoben.

In y-Richtung ist die $violette Parabel$ im Vergleich zur $grünen Parabel$ um $1,875$ (d.h. nach oben) verschoben.

Eine Veränderung des Parameters $b$ bewirkt sowohl eine Verschiebung der Parabel in x-Richtung als auch eine Verschiebung in y-Richtung.

4
Bestimme den Öffnungsfaktor und den Funktionsterm der folgenden Parabeln!

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Suche dir nun einen Punkt, den du gut vom Funktionsgraphen ablesen kannst und der nicht der Scheitelpunkt ist.
Es bietet sich der Punkt $P (2 | 2)$ an, weil da die Parabel genau eine Kästchen-Ecke trifft.
Setze die Koordinaten des Punktes $P (2 | 2)$ in die allgemeine Form für die Parabel mit dem Scheitelpunkt $S (0 | 0)$ ein.
$y = a \cdot x^{2}$
$2 = a \cdot 2^{2}$
Löse diese Gleichung nach $a$ auf!
$2 = a \cdot 4 | : 4$
$\frac{2}{4} = a$
$a = \frac{1}{2}$
Der Öffnungsfaktor hat also den Wert $a = \frac{1}{2}$ .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung $y = a \cdot x^{2}$ ein.
$y = \frac{1}{2} x^{2}$
Die Funktionsgleichung der Parabel lautet $y = \frac{1}{2} x^{2}$ .
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Suche dir nun einen Punkt, den du gut vom Funktionsgraphen ablesen kannst und der nicht der Scheitelpunkt ist.
Es bietet sich der Punkt $P (2 | 6)$ an, da da die Parabel genau die Kästchen trifft.
Setze die Koordinaten des Punktes $P (2 | 6)$ in die allgemeine Form für die Parabel mit dem Scheitelpunkt $S (0 | 0)$ ein.
$y = a \cdot x^{2}$
$6 = a \cdot 2^{2}$
Löse diese Gleichung nach $a$ auf!
$6 = a \cdot 4 | : 4$
$\frac{6}{4} = a$
$a = 1,5$
Der Öffnungsfaktor hat also den Wert $a = 1,5$ .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung $y = a \cdot x^{2}$ ein.
Damit erhältst du $y = 1,5 x^{2}$ .
Die Funktionsgleichung der Parabel lautet also $y = 1,5 x^{2}$ .
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.

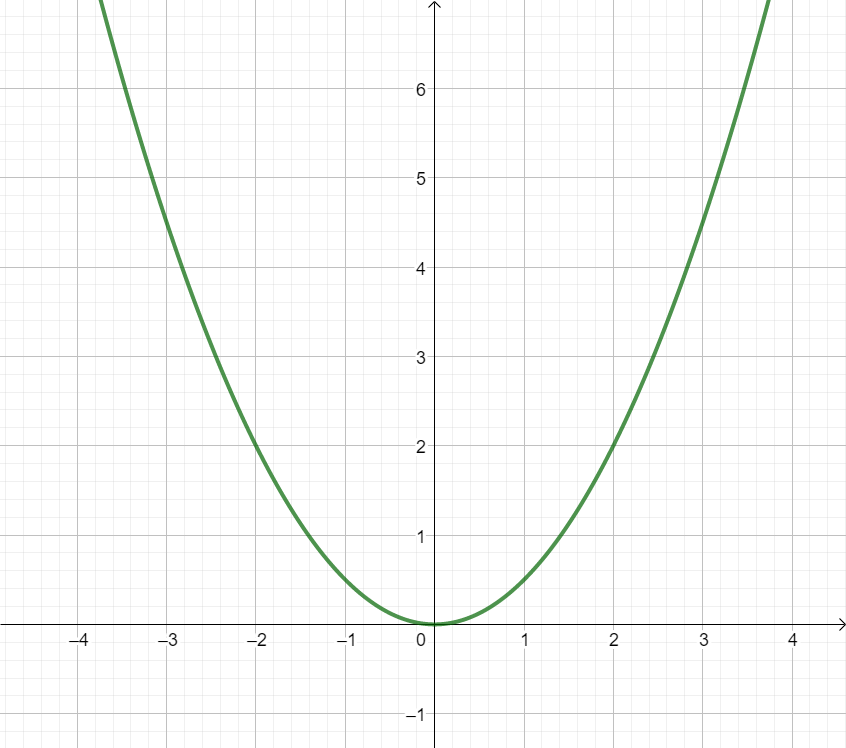
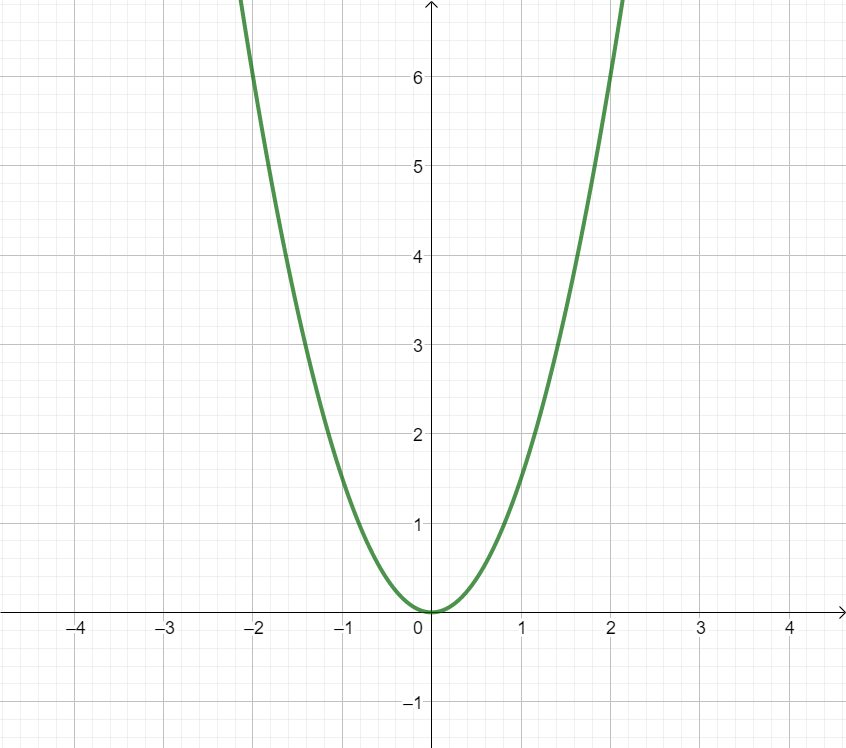
Bestimme den Funktionsterm einer Parabel mit dem Scheitelpunkt $S (0 | 0)$ , die durch den Punkt $P (3 | - 1)$ geht.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionsterm aufstellen für Parabeln
Hier berechnen wir den Funktionsterm, indem wir den Öffnungsfaktor bestimmen und mithilfe eines weiteren Punktes den Funktionsterm ausrechnen.
Um den Öffnungsfaktor der Parabel zu bestimmen benötigst du einen Punkt, der nicht der Scheitelpunkt ist. In der Angabe ist schon der Punkt $P (3 | - 1)$ gegeben.
Setze die Koordinaten des Punktes $P (3 | - 1)$ in die allgemeine Form für die Parabel mit dem Scheitelpunkt $S (0 | 0)$ ein.
$y = a \cdot x^{2}$
$- 1 = a \cdot 3^{2}$
Löse diese Gleichung nach $a$ auf!
$- 1 = a \cdot 9 | : 9$
$- \frac{1}{9} = a$
Der Öffnungsfaktor hat also den Wert $a = - \frac{1}{9}$ .
Aufstellen der Funktionsgleichung
Setze nun den Wert für den Öffnungsfaktor in die allgemeine Funktionsgleichung $y = a \cdot x^{2}$ ein.
Damit erhältst du $y = - \frac{1}{9} x^{2}$ .
Die Funktionsgleichung der Parabel lautet also $y = - \frac{1}{9} x^{2}$ .
Hier gibt es verschiedene Lösungsansatze: Du kannst z.B: 3 Punkte ablesen und daraus die Funktion bestimmen oder den Öffnungsfaktor der Parabel bestimmen und dann mit einem weiteren Punkt die Funktion ausrechnen.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das? serlo.org

Aufgaben zum Einfluss der Parameter a, b und c auf die Parabel

Lageuntersuchung der 3 Parabeln

Scheitelpunktsberechnung für f(x):

Scheitelpunktsberechnung für g(x):

Ergebnis: Wird b um 1 erhöht, so verschiebt sich der Scheitelpunkt der roten Parabel Sg(−2,25|−6,125) im Vergleich zum Scheitelpunkt der grünen Parabel Sf(−2|−4).

In x-Richtung ist die rote Parabel ist im Vergleich zur grünen Parabel um −0,25 (d.h. nach links) verschoben.

Scheitelpunktsberechnung für h(x):

Ergebnis: Wird b um 1 reduziert, so verschiebt sich der Scheitelpunkt der violetten Parabel Sh(−1,75|−2,125) im Vergleich zum Scheitelpunkt der grünen Parabel Sf(−2|−4).

In x-Richtung ist die violette Parabel ist im Vergleich zur grünen Parabel um 0,25 (d.h. nach rechts) verschoben.

Eine Veränderung des Parameters b bewirkt sowohl eine Verschiebung der Parabel in x-Richtung als auch eine Verschiebung in y-Richtung.

Aufstellen der Funktionsgleichung

Aufstellen der Funktionsgleichung

Aufstellen der Funktionsgleichung

Scheitelpunktsberechnung für $f (x)$ :

Scheitelpunktsberechnung für $g (x)$ :

Ergebnis: Wird $b$ um $1$ erhöht, so verschiebt sich der Scheitelpunkt der $roten Parabel$ $S_{g} (- 2,25 | - 6,125)$ im Vergleich zum Scheitelpunkt der $grünen Parabel$ $S_{f} (- 2 | - 4)$ .

In x-Richtung ist die $rote Parabel$ ist im Vergleich zur $grünen Parabel$ um $- 0,25$ (d.h. nach links) verschoben.

Scheitelpunktsberechnung für $h (x)$ :

Ergebnis: Wird $b$ um $1$ reduziert, so verschiebt sich der Scheitelpunkt der $violetten Parabel$ $S_{h} (- 1,75 | - 2,125)$ im Vergleich zum Scheitelpunkt der $grünen Parabel$ $S_{f} (- 2 | - 4)$ .

In x-Richtung ist die $violette Parabel$ ist im Vergleich zur $grünen Parabel$ um $0,25$ (d.h. nach rechts) verschoben.

Eine Veränderung des Parameters $b$ bewirkt sowohl eine Verschiebung der Parabel in x-Richtung als auch eine Verschiebung in y-Richtung.